Jednak nic nie rozumiem i nic z tego mi nie wyszło.
Zamykam temat bo i tak tego nie zrozumiem.
Nie poddawaj się!
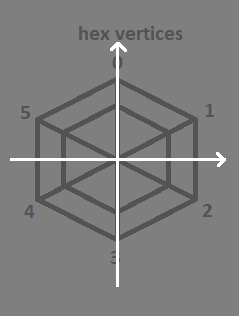
Witam. Piszę program komputerowy, który wyświetla mapę składającą się z sześciokątów. Chciałbym móc podzielić każdy sześciokąt na elementy składowe ażeby na nich operować. Potrzebuję obliczyć współrzędne v3, v4 (dla każdego z trójkątów).

Kopiuj
float outerRadius = 10.0f;
float innerRadius = outerRadius * 0.866025404f;
float n = 0.8f;
float hexVertices[ ] =
{
0.0f, outerRadius,
innerRadius, outerRadius * 0.5f,
innerRadius, - outerRadius * 0.5f,
0.0f, - outerRadius,
- innerRadius, - outerRadius * 0.5f,
- innerRadius, outerRadius * 0.5f,
0.0f, outerRadius
};
// ... --- ... //
for(int direction=0; direction<6; direction++)
{
v1x = hexVertices[2*direction] * n;
v1z = hexVertices[2*direction+1] * n;
v2x = hexVertices[2*(direction+1)] * n;
v2z = hexVertices[2*(direction+1)+1] * n;
// v3x = v1x ...
// v3z = v1z ...
// v4x = v2x ...
// v4z = v2z ...
v5x = hexVertices[2*direction];
v5z = hexVertices[2*direction+1];
v6x = hexVertices[2*(direction+1)];
v6z = hexVertices[2*(direction+1)+1];
}
- No to bierzemy obrazek:
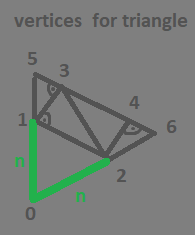
Widzisz, że wierzchołek 1 i wierzchołek 2 tworzą odcinek.
Potrzebujemy obliczyć wektor prostopadły do tego odcinka. Nazwijmy go vP.
Jak policzyć wektor prostopadły? Objaśnienie z ChatGPT masz tutaj: https://chat.openai.com/share/8c7ad73a-ae96-4251-a9b1-227f5bf88a2d
-
Otrzymany wektor prostopadły musimy znormalizować, czyli ustawić jego długość na 1.0
Potrzebne nam to będzie, aby potem łatwo ustawić długość odcinka v1=>v3, v2=>v4.
Żeby znormalizować wektor, trzeba podzielić jego składowe przez długość wektora.
Dłuższe wyjaśnienie: https://chat.openai.com/share/46d0ea92-4758-4f34-ac82-308547a5e563
-
Kiedy mamy już znormalizowany wektor, to pozostaje nam go przemnożyć przez ustaloną długość distance, która określa jak daleko od hexa mają znajdować się v3, v4.
-
Na koniec ustawiamy pozycje v3, v4. Czyli przesuwamy v1 i v2 o wektor otrzymany w poprzednich punktach.
v3 = v1 + vP;
v4 = v2 + vP;
-
Uzupełniłem zakomentowaną część Twojego kodu:
Kopiuj
float outerRadius = 10.0f;
float innerRadius = outerRadius * 0.866025404f;
float n = 0.8f;
float hexVertices[ ] =
{
0.0f, outerRadius,
innerRadius, outerRadius * 0.5f,
innerRadius, - outerRadius * 0.5f,
0.0f, - outerRadius,
- innerRadius, - outerRadius * 0.5f,
- innerRadius, outerRadius * 0.5f,
0.0f, outerRadius
};
// ... --- ... //
for(int direction=0; direction<6; direction++)
{
v1x = hexVertices[2*direction] * n;
v1z = hexVertices[2*direction+1] * n;
v2x = hexVertices[2*(direction+1)] * n;
v2z = hexVertices[2*(direction+1)+1] * n;
// wektor z v1 do v2
v12x = v2x - v1x;
v12z = v2z - v1z;
// wektor prostopadły do tego wektora
vPx = -v12z;
vPz = v12x;
// normalizacja wektora vP
float vPlength = std::sqrt(vPx * vPx + vPz * vPz);
vPx = vPx / vPlength;
vPz = vPz / vPlength;
// ustawienie długości wektora vP
vPx = vPx * distance;
vPz = vPz * distance;
// ustawienie pozycji v3, v4
v3x = v1x + vPx;
v3z = v1z + vPz;
v4x = v2x + vPx;
v4z = v2z + vPz;
v5x = hexVertices[2*direction];
v5z = hexVertices[2*direction+1];
v6x = hexVertices[2*(direction+1)];
v6z = hexVertices[2*(direction+1)+1];
}
Oczywiście musisz zadeklarować niezadeklarowane zmienne, oraz dołączyć nagłówek cmath.
Mogą się zdarzyć jakieś niedociągnięcia. Pisane bez kompilowania.