EPR paradoks - symulacja fantastyki naukowej

Jest taki słynny paradoks w fizyce kwantowej, zwany skrótem EPR - od nazwisk autorów: E to Einstein i... dwóch innych.

Nie wnikając w detale, które można sobie znaleźć w sieci, chodzi tu o to że w ramach fizyki kwantowej jest możliwe coś takiego:

https://pl.wikipedia.org/wiki/Twierdzenie_Bella

A teraz zadanie: skoro teoria (stricte matematyczna) przewiduje takie a nie inne wyniki, no to można to... zrealizować komputerowo.

Komputer to też czysta matematyka, zatem ta maszyna potrafi wszystko odtworzyć, co tylko sobie wyliczymy z teorii;
przecież matematyka nie dzieli się na komputerową i analogową - zgadza się? :)

Zapomniałem dodać, że chodzi o realistyczną symulację tych fantastycznych rewelacji,
a w szczególności i tej gry, którą opisano w załączonym linku.

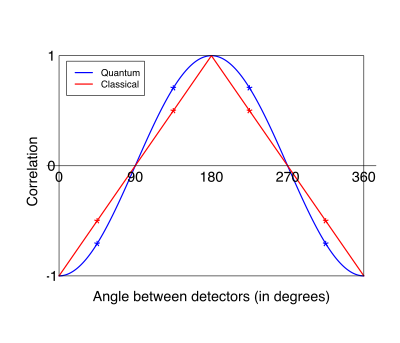
Generalnie chodzi o wygenerowanie rozkładu prawdopodobieństwa, zgodnego z QM, czyli:
##C(a,b) = -a.b/N = -cos(fa-fb);
gdzie a i b są mierzonymi seriami typu: a = {1,-1,1,1, ...};
fa i fb - to są kąty po obu stronach.

Z tego potem otrzymamy np. taki rewelacyjny wynik: cos(45) = sqrt2/2 =~ 0.7, zamiast: 0.5 zaledwie - co powinno być w ramach 'wersji klasycznej'.

Zgodnie z twierdzeniem Bella:
'Żadna lokalna teoria zmiennych ukrytych nie może opisać wszystkich zjawisk mechaniki kwantowej'.

A to moje wyniki z symulacji tego zjawiska - w lokalnym komputerku:
kąt ---- wynik - cos(kąt) = różnica
0: C=-1.0000 - -1.0000 = 0.0000; n=83.6
5: C=-0.9913 - -0.9962 = 0.0048; n=81.3
10: C=-0.9746 - -0.9848 = 0.0102; n=79.0
15: C=-0.9519 - -0.9659 = 0.0141; n=77.2
20: C=-0.9231 - -0.9397 = 0.0166; n=75.4
25: C=-0.8894 - -0.9063 = 0.0169; n=73.8
30: C=-0.8502 - -0.8660 = 0.0158; n=72.4
35: C=-0.8065 - -0.8192 = 0.0126; n=71.0
40: C=-0.7554 - -0.7660 = 0.0107; n=69.9
45: C=-0.7005 - -0.7071 = 0.0066; n=69.0
50: C=-0.6379 - -0.6428 = 0.0049; n=68.2
55: C=-0.5688 - -0.5736 = 0.0048; n=67.6
60: C=-0.4966 - -0.5000 = 0.0034; n=67.3
65: C=-0.4131 - -0.4226 = 0.0095; n=67.2
70: C=-0.3304 - -0.3420 = 0.0116; n=67.2
75: C=-0.2481 - -0.2588 = 0.0107; n=67.3
80: C=-0.1659 - -0.1736 = 0.0077; n=67.3
85: C=-0.0813 - -0.0872 = 0.0059; n=67.3
90: C=0.0002 - 0.0000 = 0.0002; n=67.3
95: C=0.0821 - 0.0872 = -0.0051; n=67.2
100: C=0.1645 - 0.1736 = -0.0092; n=67.3
105: C=0.2444 - 0.2588 = -0.0144; n=67.2
110: C=0.3312 - 0.3420 = -0.0108; n=67.3
115: C=0.4128 - 0.4226 = -0.0098; n=67.3
120: C=0.4973 - 0.5000 = -0.0027; n=67.2
125: C=0.5704 - 0.5736 = -0.0031; n=67.6
130: C=0.6386 - 0.6428 = -0.0042; n=68.1
135: C=0.6994 - 0.7071 = -0.0077; n=68.9
140: C=0.7537 - 0.7660 = -0.0124; n=70.1
145: C=0.8058 - 0.8192 = -0.0133; n=71.1
150: C=0.8499 - 0.8660 = -0.0161; n=72.4
155: C=0.8893 - 0.9063 = -0.0171; n=73.9
160: C=0.9237 - 0.9397 = -0.0160; n=75.4
165: C=0.9512 - 0.9659 = -0.0148; n=77.1
170: C=0.9747 - 0.9848 = -0.0101; n=79.0
175: C=0.9911 - 0.9962 = -0.0051; n=81.2
180: C=1.0000 - 1.0000 = 0.0000; n=83.6

błędy na poziomie 1% zaledwie, czyli Bell był głupi jak but - moje twierdzenie brzmi tak:
cokolwiek głupek sobie wymyśli, to komputer i tak wyliczy.

wil napisał(a):

Komputer to też czysta matematyka, zatem ta maszyna potrafi wszystko odtworzyć, co tylko sobie wyliczymy z teorii;
przecież matematyka nie dzieli się na komputerową i analogową - zgadza się? :)

Nie zgadza się. ;)

Zastosowałeś wynikanie w złą stronę. Komputer to czysta matematyka, więc wszystko, co dzieje się w komputerze można opisać matematycznie, ale nie wszystko matematyczne można opisać komputerowo... Matematyka jest większa/silniejsza (w sensie: ogólniejsza).

Zależy od programisty - marny programista to marny matematyk.
Przecież komputer może symulować nawet człowieka - świadomość, itd. więc o czym tu mowa?

Zatem: cokolwiek wymyślisz w ramach dowolnej teorii, opisanej formalnie = matematycznie,
to samo i komputer może zrobić (w ramach symulacji).

Zadanie extra: co reprezentuje ostatnia kolumna w wynikach, który tam podałem?

Tam są liczby oznaczone n=, które biegną od 83 do 67 około;
to są liczby koincydencji w procentach, czyli liczba uzyskanych pomiarów podczas testu - no, ale co to za funkcja?

wil napisał(a):

Przecież komputer może symulować nawet człowieka - świadomość, itd. więc o czym tu mowa?

To akurat raczej nie jest prawda. Szczególnie, że nie masz żadnego przykładu komputera, który jak piszesz "może symulować nawet człowieka - świadomość, itd."... Chyba, że nie wiem, że w międzyczasie jakiś powstał... :/

Co więcej, pewne wyniki matematyczne sugerują, że komputer (przynajmniej taki, jaki dziś znamy, czyli zgodny z maszyną Turinga) NIE może symulować człowieka:
https://pl.wikipedia.org/wiki/Argument_Lucasa-Penrose%E2%80%99a

Zatem: cokolwiek wymyślisz w ramach dowolnej teorii, opisanej formalnie = matematycznie,
to samo i komputer może zrobić (w ramach symulacji).

Patrz wyżej.

koszalek-opalek napisał(a):

wil napisał(a):

Przecież komputer może symulować nawet człowieka - świadomość, itd. więc o czym tu mowa?

To akurat raczej nie jest prawda. Szczególnie, że nie masz żadnego przykładu komputera, który jak piszesz "może symulować nawet człowieka - świadomość, itd."... Chyba, że nie wiem, że w międzyczasie jakiś powstał... :/

Co więcej, pewne wyniki matematyczne sugerują, że komputer (przynajmniej taki, jaki dziś znamy, czyli zgodny z maszyną Turinga) NIE może symulować człowieka:
https://pl.wikipedia.org/wiki/Argument_Lucasa-Penrose%E2%80%99a

Zatem: cokolwiek wymyślisz w ramach dowolnej teorii, opisanej formalnie = matematycznie,
to samo i komputer może zrobić (w ramach symulacji).

Patrz wyżej.

Penrose należy do klubu Bella... pseudomatematyków nieoznaczonych. :)

Nie potrafili wyliczyć, ani też wytłumaczyć - uzasadnić, tych korelacji, więc niestworzone rzeczy wymyślali.

To sobie poczytaj:
http://libertesphilosophica.info/blog/

C(a,b) = -a.b/N = -cos(fa-fb);
gdzie a i b są mierzonymi seriami typu: a = {1,-1,1,1, ...};
fa i fb - to są kąty po obu stronach.

Zdefiniuj przestrzeń w ramach, której te operacje przeprowadzasz, to będzie można coś powiedzieć o Twoich symulacjach.

• a+a wydają się nie należeć do przestrzeni ciągów {1,-1,...}, więc wspomniane ciągi nie tworzą przestrzeni liniowej, zaś iloczyn skalarny nie ma sensu na nieliniowej przestrzeni? :P
  No chyba, że definiujesz go inaczej, to napisz jak.
• fa, fb - kąty po obu stronach "czego" i czym jest "strona"?
• Jakie jest kryterium stopu tej symulacji?
• Jaki rozkład ma a_i?
• Czy wszystkie elementy a są != 0, czy tylko skończenie wiele.
• Jak liczysz odległość między wektorami a i b ? Metryka Minkowskiego czy jakaś inna?

Korelację C(a,b) wyliczamy po prost tak:
zgodne - niezgodne / (zgodne + niezgodne)

gdzie: zgodne to takie gdy są równe, znaczy: a[i] = b[i], czyli 1 i 1 lub -1 i -1;
natomiast niezgodne: a[i] <> b[i], czyli 1 i -1 lub -1 i 1;

więc można to zapisać tak:
N-- + N++ - N-+ - N+- / N; gdzie N = N-- + N++ + N-+ + N+-;

ale to samo otrzymamy gdy zwyczajnie wymnożymy te 'wektory', ponieważ nietrudno zauważyć że:
a[i].b[i] = 1 => a[i] = b[i], oraz a[i].b[i] = -1 => a[i] != b[i]"

.....
Zadanie polega na wygenerowaniu funkcji -cos(fa-fb), z dwóch niezależnie generowanych serii a i b;
w praktyce jest to mierzone zdalnie na dwóch stanowiskach (polaryzatorach): A i B w innym miejscu, i A nie wie nic o stanie i wynikach B, i odwrotnie.

Skrótowo: należy wygenerować tę funkcję, której wynik zależy od dwóch parametrów po obu stronach: fa i fb,
jednak podczas generowania 'a' nie mamy dostępu do fb, natomiast w b nie znamy fa!

Tak to ma wyglądać:

Wybacz, że fizyki nie rozumiem i powoli łapię coś co dla Ciebie może być oczywiste, stąd też dużo pytań ;-)

• Jak rozumiem mierzysz pewną wielkość na 2 stanowiskach?
• Jak symulujesz błąd pomiarowy w programie komputerowym? Zakładasz jakiś szczególny rozkład tego błędu ?
• Jeśli A jest serią, to czym jest FA ? Wartością funkcji cosX w punkcie A_I ?
• Ile tych pomiarów wykonujesz? Tzn. jakie jest N i kiedy uznajesz, że N jest wystarczające do symulacji?
• Jeśli mamy 2 stanowiska, to czym jest kąt między nimi ?
• KIedy mówimy, że a[i] i b[i] są zgodne jeśli wykonamy I-ty pomiar w lokalizacji A i B, to a[i] i b[i] są zgodne jeśli różnią się o
  jakąś przyjętą wartość? Jaką?

yarel napisał(a):

Wybacz, że fizyki nie rozumiem i powoli łapię coś co dla Ciebie może być oczywiste, stąd też dużo pytań ;-)

• Jak rozumiem mierzysz pewną wielkość na 2 stanowiskach?
• Jak symulujesz błąd pomiarowy w programie komputerowym? Zakładasz jakiś szczególny rozkład tego błędu ?
• Jeśli A jest serią, to czym jest FA ? Wartością funkcji cosX w punkcie A_I ?
• Ile tych pomiarów wykonujesz? Tzn. jakie jest N i kiedy uznajesz, że N jest wystarczające do symulacji?
• Jeśli mamy 2 stanowiska, to czym jest kąt między nimi ?
• KIedy mówimy, że a[i] i b[i] są zgodne jeśli wykonamy I-ty pomiar w lokalizacji A i B, to a[i] i b[i] są zgodne jeśli różnią się o
  jakąś przyjętą wartość? Jaką?

Detektor mierzy tu tylko dwa stany: 1 - zarejestrowano impuls, albo 0 - nie stwierdzono impulsu.

W symulacji używam różne N - im większe tym lepiej; zwykle używam N = milion,
wtedy obliczenia trwają kilka sekund, a błędy są na poziomie 1%;
to jest symulacja typu Monte Carlo, więc błąd tu maleje jak: 1/sqrt(N).

Kąty są dwa, po jednym na stanowisko - w praktyce jest to ustawienie polaryzatora.

W praktyce te serie są losowe, to znaczy gdy wyliczysz: p(+1) = 1/2, i p(-1) = 1/2, w obu seriach: a i b;
(przez polaryzator przechodzi 50% światła niespolaryzowanego - losowych fotonów).

Rozkłady błędów pomiarowych, głównie braki koincydencji w obu pomiarach naraz,
są tu właśnie kluczem do wygenerowania poprawnego wyniku, czyli właśnie to trzeba tu 'zgadnąć'...

W zasadzie nie ma tu czego 'zgadywać', ponieważ tu dowolna metoda produkuje wyniki 'nieklasyczne'. :)
Po prostu: dowolny błąd powoduje tu odchyłkę od tych 'klasycznych' korelacji.

Czy ty nie zabierasz się do tego od złej strony?
Żeby otrzymać wyniki podane w tej teorii, mierzone cząsteczki muszą być w stanie splątania kwantowego, czego nie osiągniesz na klasycznym komputerze.
Tutaj natomiast jedyne co otrzymałeś to kosinus dla podanego kąta.

Świetny Terrorysta napisał(a):

Czy ty nie zabierasz się do tego od złej strony?
Żeby otrzymać wyniki podane w tej teorii, mierzone cząsteczki muszą być w stanie splątania kwantowego, czego nie osiągniesz na klasycznym komputerze.

Zakładam 'splątanie' par cząstek, czyli perfekcyjną antykorelację spinów: s1 + s2 = 0,
co bardzo łatwo osiągnąć w komputerze, o tak: s1 = -s2.

Tutaj natomiast jedyne co otrzymałeś to kosinus dla podanego kąta.

Bo na tym to polega: C(a,b) = -cos(a-b), wedle QM,
a reszta to już tylko konsekwencje tej korelacji.