Regresja liniowa

Regresja liniowa [stat], [mat] to metoda estymowania wartości oczekiwanej zmiennej y przy znanych wartościach innej zmiennej lub zmiennych x. Szukana zmienna, y, jest tradycyjnie nazywana zmienną zależną. Inne zmienne x nazywa się zmiennymi niezależnymi. Zarówno zmienne zależne, jak i niezależne, mogą być wielkościami skalarnymi lub wektorami.

Regresja w ogólności to problem estymacji warunkowej wartości oczekiwanej. Regresja liniowa jest nazywana liniową, gdyż relacja między zmiennymi zależnymi, a niezależnymi, jest funkcją liniową.

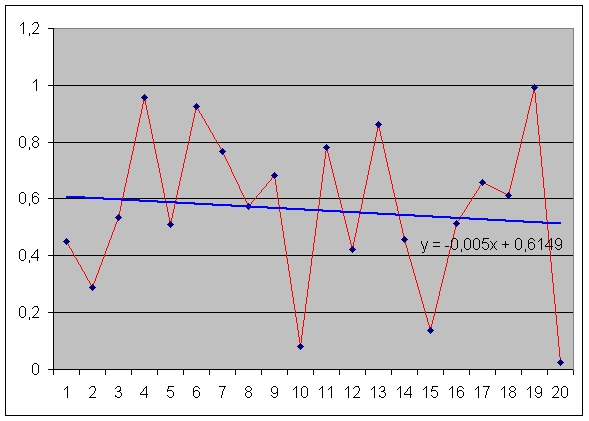
Wykresem regresji liniowej jest prosta, która jak najlepiej "pasuje" do zbioru danych.

Najprostszą metodą jest metoda najmniejszych kwadratów. Ma ona jednak zasadniczą wadę w postaci małej odporności na wyniki skrajne. Metoda najmniejszych kwadratów opiera się na warunku:

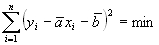
Gdzie a i b są emiprycznymi współczynnikami regresji liniowej. Jak łatwo zauważyć, wyrażenie w nawiasie w tym równaniu jest odchyleniem punktu eksperymentalnego (liczonym wzdłuż osi y) od odpowiadającej mu wartości wynikającej z równania prostej. Poszukując ekstremum związanego powyższego równania udowadnia się, że:

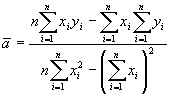
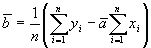
Implementacja funkcji (Procedury) obliczającej regresję może być następująca:

procedure RegLin(DBx, DBy : array of Double; var A, B :Double);
var
  SigX, SigY : Double; { sumy liczb }
  SigXY : Double;
  SigSqrX : Double;
  n, i : Word;   { liczba elementów tablic }
begin
  n := High(DBx) + 1; { określamy liczbę elementów }
  SigX := 0; SigY := 0;
  SigXY := 0;
  SigSqrX := 0;

  for i := 0 to n-1 do
  begin
    SigX := SigX + DBx[i];
    SigY := SigY + DBy[i];
    SigXY := SigXY + (DBx[i] * DBy[i]);
    SigSqrX := SigSqrX + Sqr(DBx[i]);
  end;
 
  A := (n * SigXY - SigX * SigY) / (n * SigSqrX - Sqr(Sigx));
  B := 1/n * (SigY - A * SigX);
end;

Jak widać w nagłówku jako rezultat obliczeń procedura zwraca współczynniki równania prostej y = ax+b.

Źródła informacji: Wikipedia, MS Excel help

Zobacz też:

• Interpolacja liniowa