Trygonometria sferyczna - długość odcinka

Sferyczna powierzchnia kuli nie może być odwzorowana na płaszczyźnie bez zniekształceń; również odległość pomiędzy dwoma punktami ulega zniekształceniom. Jedynie w przypadku wielkoskalowych odwzorowań, obejmujących mały wycinek powierzchni, sferyczne zakrzywienie odgrywa znikomą rolę. Pomiar dużej odległości na małoskalowych odwzorowaniach daje wielkie błędy. W tych przypadkach dla wyznaczenia właściwej odległości między dwoma punktami stosuje się formuły trygonometrii sferycznej.

Ten sposób określania odległości wymaga podejścia bardziej geograficznego niż programistycznego, a mianowicie wymaga znajomości współrzędnych: szerokość i długość geograficzną dwóch punktów . Oznaczamy je: lambda - długość, fi - szerokość.

Do wyznaczenia długości stosuje się wzór:

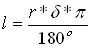
Do wyznaczenia deltyy stosuje się wzór:

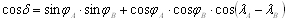
gdzie:
l - odległość A-B
r - promień kuli
delta- kąt środkowy

Ponieważ komputery wolą radiany, wartość należy skorygować w następujący sposób:

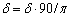
Aby móc przeprowadzić obliczenia w delphi należy użyć modułu Math. W przypadku Turbo Pascala, należy zadeklarować funkcję arcus cosinus. Oblicza się ją w następujący sposób (z uwzględnieniem konwersji radianów na stopnie):

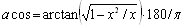
Oto przykładowa implementacja funkcji:

function ArcCos(X: Double): Double;
begin
  ArcCos := ArcTan(Sqrt(1 - Sqr(X)) / X;
end;

Funkcja zwracająca długość odcinka może mieć postać:

// f - to fi
// l - to lambda
// r - promień kuli
function Len(fA, fB, lA, lB, r: Double): Double;
var
  delta: Double;
begin
  delta := Sin(fA) * Sin(fB) + Cos(fA) * Cos(fB) * Cos(lA ? lB);
  delta := ArcCos(delta) * 90 / Pi;
  Len := r * delta * Pi / 180;
end;

Ważne aby kąt podawać nie w formacie stopień.minuta tylko w postaci dziesiętnej. Jeżeli chcemy użyć minut konieczne byłyby dalsze przekształcenia.