Współrzędne
Riddle
Artykuł jest przeznaczony dla zarówno dla początkujących kodziarzy, jak i również dla tych ze stażem. Przykłady tutaj pokazane będą w językach Pascal i C++ ale z powodzeniem mogą zostać przetłumaczone na inne języki bez większych problemów.
Więc zaczynamy!
Na początek zadeklarujmy sobie strukturę TPoint (w Delphi jest ona w module Types, w C++ jej nie ma):
struct TPoint
{
int x, y;
};
Oraz funkcję sqr (podnosi ona wartość do kwadratu):
float sqr(float n)
{
return n*n;
}
Obliczanie odległości między dwoma punktami w układzie współrzędnych
Każde okienko jest swego rodzaju układem współrzędnych z tym, że różni się od tradycyjnego tylko tym, że oś Y inkrementuje w dół, a w tradycyjnym w górę. Więc nie ma żadnych przeszkód, aby używać zwyczajnych funkcji trygonometrycznych. Po tym małym wstępie przechodzimy dalej, czyli do obliczania odległości. W tym celu posłużę się troszku zmienionym twierdzeniem Pitagorasa. Załóżmy chcemy obliczyć odległość między tymi dwoma punktami.
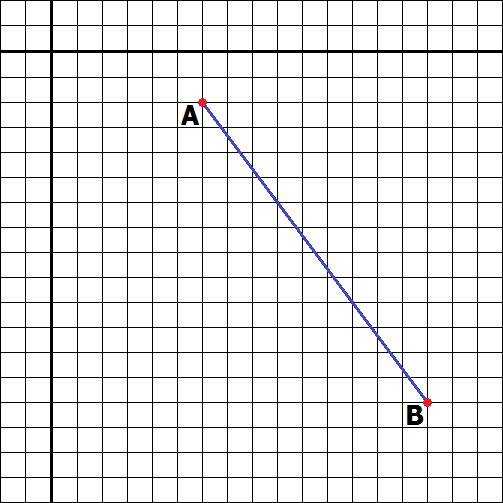
Wystarczy wyobrazić sobie, że ta linia to trzeci bo trójkąta prostokątnego.
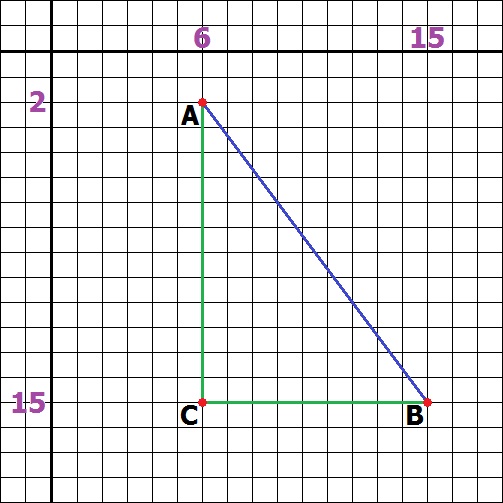
I teraz przeprowadzamy bardzo proste obliczenia:
function GetDistance(A, B: TPoint): Extended;
var FlankA, FlankB, FlankC: Extended;
begin
FlankA := A.Y - B.Y; //Długość boku A
FlankB := A.X - B.X; //Długość boku B
{To nic że wartości mogą być ujemne, gdyż później podniesiemy je do kwadratu}
FlankC := Sqrt( //Pierwiastek z...
Sqr(FlankA) //...bok A do kwadratu...
+ //...plus...
Sqr(FlankB) //...bok B do kwadratu.
);
Result := FlankC;
end;
float GetDistance (TPoint A, TPoint B)
{
float FlankA = A.Y - B.Y; //Długość boku A
float FlankB = A.X - B.X; //Długość boku B
// To nic że wartości mogą być ujemne, gdyż później podniesiemy je do kwadratu
float FlankC = sqrt( //Pierwiastek z...
sqr(FlankA) //...bok A do kwadratu...
+ //...plus...
sqr(FlankB) //...bok B do kwadratu.
);
return FlankC;
}
W przykładzie powyżej użyłem więcej zmiennych, niżeli jest to konieczne, aby zobrazować na czym polega rozwiązanie. Równie dobrze można ten zapis uprościć do takiej postaci:
function GetDistance(A, B: TPoint): Extended;
begin
Result := Sqrt(Sqr(A.Y - B.Y) + Sqr(A.X - B.X) );
end;
float GetDistance(TPoint A, TPoint B)
{
return sqrt(sqr(A.Y - B.Y) + sqr(A.X - B.X));
}
Odnajdywanie punktu
Teraz zajmiemy się czymś troszku innym, a mianowicie odnajdywaniem takiego punktu B, który jest na określonej odległości od punktu A i pod określonym kątem.
uses Math;
const
Pi = 3.1415;
function FindPoint(A: TPoint; Distance, Angle: Integer); TPoint;
begin
Result.X := Round(A.X + Distance * Sin(Angle / 180 * Pi));
Result.Y := Round(A.Y + Distance * Cos(Angle / 180 * Pi));
end;
#include <math.h>
#define PI 3.1415
TPoint FindPoint(TPoint A, int Distance, int Angle)
{
TPoint point
point.X = round(A.X + Distance * sin(Angle / 180 * Pi));
point.Y = round(A.Y + Distance * cos(Angle / 180 * Pi));
return point;
}
Właściwie nie wiem jak mógłbym wytłumaczyć ten kod, po prostu działa i już ;)
Obliczanie kąta
Można bardzo prosto przerobić powyższy kod do takiej postaci:
Więc:
function GetAngle(A, B: TPoint): Extended;
var Distance, Angle: Extended;
begin
Distance := GetDistance(A, B); //Funkcja z wcześniejszej części artykułu
Angle := ArcCos((B.Y - A.Y) / Distance) * 180 / Pi;
Result := Angle;
end;
float GetAngle (TPoint A, TPoint B)
{
float distance = GetDistance(A, B); //Funkcja z wcześniejszej części artykułu
float angle = acos((B.Y - A.Y) / distance) * 180 / Pi;
return angle;
}
Ten kod posłuży do znalezienia @@a@@
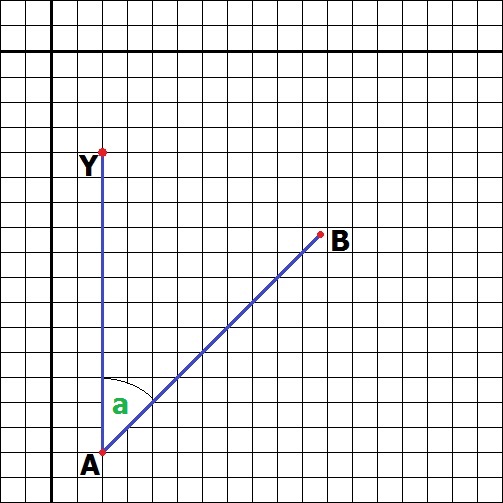
Powyższy kod obliczy kąt z przedziału 0-180 stopni z każdej strony. Jeżeli chcemy obliczyć, kąt z przedziału 0-360 stopni, należy dodać linijkę
if B.X < A.X then Angle := 360 - Angle;
if (B.X < A.X) angle = 360 - angle;
Warto zauważyć że ten kod obliczy jedynie kąt między osią Y a linią |AB|. Żeby, natomiast, obliczyć kąt pomiędzy dowolnymi trzema punktami...
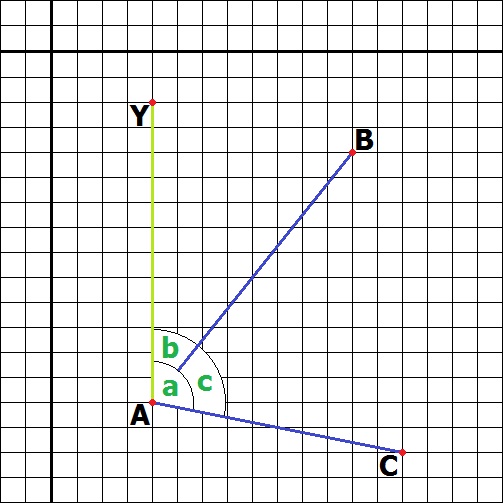
...należy najpierw obliczyć kąt pomiędzy osią Y a linią |AB|, potem między osią Y a linią |AC| a potem je od siebie odjąć.
function GetAngle(A, B, C: TPoint): Extended; overload;
begin
Result := GetAngle(A, C) - GetAngle(B, A);
end;
float GetAngle (TPoint A, TPoint B, TPoint C)
{
return GetAngle(A, C) - GetAngle(B, A);
}
Zastrzegam sb prawo do tego artykułu i nie zgadzam sie na publikowanie go gdziekolwiek bez mojej wiedzy.
ładny art :)
Poprawione :)
Poprawiamy...
U mnie też nie ma, nie wiem czemu.
Czy tylko u mnie w artykule nie ma obrazków? Ale na podglądzie podczas edycji już są.