Interpreter równań
msm
Wstęp
Natrafiłem niedawno na artykuł Interpreter równań (Delphi). Problem mnie zaciekawił i postanowiłem napisać własną wersję tamtego programu. Cóż, moim zdaniem tamten program jest dużo lepszy -.- ...
Ok, przejdźmy od teorii do praktyki, czyli kodu. Idea mojego kodu polega na tym, że dowolne równanie podane przez użytkownika (jako string, oczywiście) program "rozbija" sobie na drzewo. 'Drzewo' to składa się z węzłów i połączeń między nimi.
Rozbijanie na drzewo
Przykład rozbitego na drzewo równania:
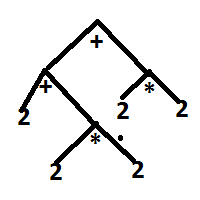
Mój program robi to rekurencyjnie. Ponieważ trudno mi opisać dokładnie o co chodzi operując tylko na teorii, posłużę się przykładem:
Oto równanie które będziemy interpretować:
0: 2+22+22
Na początku znajdujemy miejsce gdzie należy "przedzielić" równanie. Chodzi o to, żeby na samym szczycie równania były działania wykonywane na końcu. Znajdujemy je:
1: 2+22+22
i dzielimy równanie na dwie części:
2: 2+22 i 22
a znak wzdłuż którego przedzieliliśmy bierzemy za wykonywane działanie. Mamy już pierwszy węzeł! Dalej analogicznie
3: 2+22 i 22
4: 2 i 2*2 i 2 i 2
5: 2 i 2 i 2 i 2 i 2.
Co w sumie daje nam drzewo przedstawione na rysunku
Źródło:
Kod rozbiłem sobie na kilka klas:
- EQU_tree - abstrakcyjny główny węzeł drzewa. Nie ma żadnej wartości tylko jest uchwytem do równania.
- TreeNode - zwykły węzeł drzewa. Zawiera dwa połączenia i działanie.
- ConnExtented - połączenie między węzłami.
- ConnSmple - 'połączenie' między węzłem a wartością - przechowuje on po prostu wartość liczbową.
- TreeConn - klasa bazowa dla dwóch powyższych
- Functions - klasa zawierająca listę dostępnych działań.
Oto i one (ponieważ do wszystkich klas dopisane są komentarze, ośmieliłem się nie dodawać nic od siebie w tekście.
EQU_Tree
/// <summary>
/// Główny węzeł równania. Stanowi w pewien
/// sposób 'uchwyt' dla zewnętrznych funkcji,
/// tylko do niego można się bezpośrednio odnosić.
/// </summary>
class EQU_tree
{
private TreeConn root;
private Functions functions;
private EquResult result;
/// <summary>
/// Tworzy nową pustą instancję równania.
/// </summary>
public EQU_tree()
{
functions = new Functions(true);
}
/// <summary>
/// Tworzy drzewo równania z podanego łańcucha
/// </summary>
/// <param name="equality">Równanie.</param>
/// <returns>Wynik operacji (błąd).</returns>
public EquResult CreateTree(string equality)
{
equality = Convert(equality);
result = ValidateInput(equality);
if (result.ErrorCode == EquErrors.ArgumentEmpty) equality = "0";
if (!result.IsAllowed) return result;
root = TreeConn.Create(equality, this, ref result);
return result;
}
/// <summary>
/// Sprawdza czy wartości podane przez użytkownika są poprawne
/// (oczywiście tylko najbardziej oczywiste możliwe błędy)
/// </summary>
private EquResult ValidateInput(string equality)
{
if (equality == null) return new EquResult(EquErrors.ArgumentNull);
if (equality == "") return new EquResult(EquErrors.ArgumentEmpty);
if (Regex.Matches(equality, @"\(").Count !=
Regex.Matches(equality, @"\)").Count)
return new EquResult(EquErrors.NotValidBrackets);
return new EquResult(EquErrors.None);
}
/// <summary>
/// Zamienia popularnie używane przez niektórych
/// symbole na rozpoznawalne przez funkcję.
/// </summary>
private string Convert(string equality)
{
equality = equality.Replace(" ", "");
equality = equality.Replace(".", ",");
equality = equality.Replace("[", "(");
equality = equality.Replace("]", ")");
return equality;
}
/// <summary>
/// Wylicza wartość równania. Za każdym razem wyliczanie
/// jest wykonywane od nowa!
/// </summary>
/// <param name="result">Wynik operacji (zmieniany gdy błąd).</param>
/// <returns>Wynik.</returns>
public double Calculate(out EquResult result)
{
result = new EquResult(EquErrors.None);
return root.Calculate(ref result);
}
/// <summary>
/// Zwraca listę zarejestrowanych funkcji.
/// </summary>
internal Functions GetFunctions
{ get { return functions; } }
/// <summary>
/// Dodaje nową funkcję.
/// </summary>
/// <param name="id">Łańcuch przedstawiający fukcję, pod jakim ma
/// być identyfikowana (np. '+' dla dodawania, '/' dla dzielenia etc.</param>
/// <param name="action">Delegacja do funkcji wykonywanej dla działania</param>
/// <param name="rank">Ważność funkcji w kolejności wykonywania działań.
/// (im niższa tym ważniejsza)</param>
public EquResult AddFunction(string id, Function action, uint rank)
{
EquResult r = functions.AddFunction(id, action, rank);
return r;
}
}
TreeNode
/// <summary>
/// Klasa reprezentująca 'węzeł' drzewa równań.
/// Definiuje dwa połączenia (do pierwszego i drugiego
/// wyrazu działania) i znak działania.
/// </summary>
class TreeNode
{
EQU_tree parent;
/// <summary>
/// Tworzy nową instancję węzła.
/// </summary>
/// <param name="equality">Równanie z którego utworzyć węzeł.</param>
/// <param name="parent">Referencja do głównego węzła</param>
/// <param name="result">Wynik operacji (zmieniany gdy błąd)</param>
public TreeNode(string equality, EQU_tree parent, ref EquResult result)
{
this.parent = parent;
int start;
int lenght;
parent.GetFunctions.FindNext(equality, out start, out lenght, ref result);
if (start < 0)
{
result = new EquResult(EquErrors.NoSuitableDivide);
return;
}
Conn1 = TreeConn.Create(equality.Substring(0, start), parent, ref result);
Conn2 = TreeConn.Create(equality.Substring(start + lenght), parent, ref result);
Operation = equality.Substring(start, lenght);
}
/// <summary>
/// Wylicza i zwraca wyliczoną wartość węzła
/// </summary>
/// <param name="result">Wynik (zmieniany gdy błąd)</param>
public double Calculate(ref EquResult result)
{
double value = 0;
try
{
double conn1value = Conn1.Calculate(ref result);
if (result.IsFatal) { return conn1value; }
double conn2value = Conn2.Calculate(ref result);
if (result.IsFatal) { return value; }
value = parent.GetFunctions.Calculate(Operation.ToString(), conn1value, conn2value, ref result);
}
catch (System.NullReferenceException)
{
result = new EquResult(EquErrors.NullConnection);
}
catch (System.OverflowException)
{
result = new EquResult(EquErrors.Overflow);
}
catch (System.ArgumentException)
{
result = new EquResult(EquErrors.InvalidOperation);
}
return value;
}
/// <summary>
/// Pierwsze połączenie (wyraz działania)
/// </summary>
public TreeConn Conn1
{ get; set; }
/// <summary>
/// Drugie połączenie (wyraz działanie)
/// </summary>
public TreeConn Conn2
{ get; set; }
/// <summary>
/// Operacja (działanie)
/// </summary>
public string Operation
{ get; set; }
}
ConnSimple
/// <summary>
/// Reprezentuje proste 'połączenie' - nie odnosi się
/// do innego węzła tylko przechowuje wartość.
/// </summary>
class ConnSimple : TreeConn
{
/// <summary>
/// Wartość przechowywana przez połączenia.
/// </summary>
public double Value
{ get; set; }
/// <summary>
/// Wylicza wartość połączenia - w tym przypadku po prostu zwraca wartość.
/// </summary>
/// <param name="result">Wynik operacji (zmieniany gdy błąd)</param>
/// <returns></returns>
public override double Calculate(ref EquResult result)
{
return Value;
}
}
ConnExtented
/// <summary>
/// Reprezentuje rozszerzone połączenie - przechowuje
/// węzeł do którego się odnosi.
/// </summary>
class ConnExtented : TreeConn
{
/// <summary>
/// Węzeł do którego 'łączy się' ten obiekt.
/// </summary>
public TreeNode Node
{ get; set; }
/// <summary>
/// Tworzy nową instancję rozszerzonego połączenia.
/// </summary>
/// <param name="equality">Równanie z którego utworzyć węzeł</param>
/// <param name="parent">Referencja do głównego węzła.</param>
/// <param name="result">Wynik operacji (zmieniany gdy błąd)</param>
public ConnExtented(string equality, EQU_tree parent, ref EquResult result)
{
Node = new TreeNode(equality, parent, ref result);
}
/// <summary>
/// Wylicza wartość połączenia - w tym przypadku nakazuje
/// potomnemu węzłowi wyliczyć swoją wartość.
/// </summary>
/// <param name="result">Wynik operacji (zmieniany gdy błąd)</param>
public override double Calculate(ref EquResult result)
{
return Node.Calculate(ref result);
}
}
TreeConn
/// <summary>
/// Abstrakcyjna klasa bazowa dla ConnSimple i ConnExtented -
/// definiuje podstawowe metody dla obydwóch.
/// </summary>
abstract class TreeConn
{
public abstract double Calculate(ref EquResult result);
/// <summary>
/// Tworzy obiekt abstrakcyjnej klasy TreeConn i zwraca go.
/// </summary>
/// <param name="equality">Równanie.</param>
/// <param name="parent">Referencja do podstawowego węzła</param>
/// <param name="result">Wynik operacji (zmieniany gdy błąd)</param>
public static TreeConn Create(string equality, EQU_tree parent, ref EquResult result)
{
equality = RemoveBrackets(equality, ref result);
bool parsers;
double value;
parsers = double.TryParse(equality, out value);
TreeConn connection;
if (parsers == true)
{
connection = new ConnSimple() { Value = value };
}
else
{
connection = new ConnExtented(equality, parent, ref result);
}
return connection;
}
/// <summary>
/// Usuwa nieprzwidłowe nawiasy z łańcucha
/// </summary>
/// <param name="equality">Równanie</param>
/// <param name="result">Wynik operacji (zmieniany gdy błąd)</param>
private static string RemoveBrackets(string equality, ref EquResult result)
{
//Może niezbyt wyrafinowany sposób usuwania nieprawidłowych nawiasów...
if (Regex.IsMatch(equality, "[()]+[^()]+"))
{
while (equality.StartsWith("(") || equality.StartsWith(")"))
equality = equality.Remove(0, 1);
}
if (Regex.IsMatch(equality, "[^()]+[()]+"))
{
while (equality.EndsWith("(") || equality.EndsWith(")"))
equality = equality.Remove(equality.Length - 1);
}
if (Regex.IsMatch(equality, "[()]+.+[()]+"))
{
while((equality.StartsWith("(") || equality.StartsWith(")"))
&& (equality.EndsWith("(") || equality.EndsWith(")")))
equality = equality.Substring(1, equality.Length - 2);
}
return equality;
}
}
Functions
/// <summary>
/// Delegacja reprezentująca funkcję (a raczej działanie) wykonywaną w równaniu
/// </summary>
/// <param name="value1">Wartość pierwsza działania.</param>
/// <param name="value2">Wartość druga działania.</param>
public delegate double Function(double value1, double value2);
class Functions
{
private Dictionary<string, Function>[] symbols;
//private Dictionary<string, Function> symbols;
/// <summary>
/// Tworzy nowy zestaw funkcji.
/// </summary>
/// <param name="defvalues">Czy dodać domyślny zbiór funkcji?</param>
public Functions(bool defvalues)
{
this.symbols = new Dictionary<string, Function>[5];
this.InitializeSymbols();
if (defvalues) this.InitializeDefault();
}
/// <summary>
/// Inicjalizuje wszystkie słowniki w liście ważności.
/// </summary>
private void InitializeSymbols()
{
for(int i = 0; i < symbols.Length; i++)
symbols[i] = new Dictionary<string,Function>();
}
/// <summary>
/// Dodaje domyślny zbiór funkcji.
/// </summary>
private void InitializeDefault()
{
symbols[3].Add("+", new Function(Addition));
symbols[3].Add("-", new Function(Substraction));
symbols[2].Add("*", new Function(Multiplication));
symbols[2].Add("/", new Function(Division));
}
#region Default functions
/// <summary>
/// Default function: addition.
/// </summary>
private double Addition(double value1, double value2)
{
return value1 + value2;
}
/// <summary>
/// Default function: substraction.
/// </summary>
private double Substraction(double value1, double value2)
{
return value1 - value2;
}
/// <summary>
/// Default function: multiplication.
/// </summary>
private double Multiplication(double value1, double value2)
{
return value1 * value2;
}
/// <summary>
/// Default function: division.
/// </summary>
private double Division(double value1, double value2)
{
return value1 / value2;
}
#endregion
/// <summary>
/// Dodaje nową funkcję do listy.
/// </summary>
/// <param name="id">Łańcuch pod którym funkcja będzie identyfikowana.
/// Nie może zawierać liczb.</param>
/// <param name="action">Funkcja wywoływana dla id.</param>
/// <param name="rank">Ważność w kolejności wykonywania działań
/// (im niższa tym funkcja ważniejsza)</param>
/// <returns></returns>
public EquResult AddFunction(string id, Function action, uint rank)
{
// Jeśli zawiera jakąś cyfrę...
if (System.Text.RegularExpressions.Regex.Matches(id, @"\d").Count != 0)
return new EquResult(EquErrors.IncorrectFunctionName);
// Jeśli ranga jest za duża...
if (symbols.Length <= rank)
return new EquResult(EquErrors.InvalidRank);
// Jeśli nazwa już zajęta...
if (symbols[rank].ContainsKey(id))
return new EquResult(EquErrors.MultipledFunctionName);
symbols[rank].Add(id, action);
return new EquResult(EquErrors.None);
}
/// <summary>
/// Wylicza wartość dla dwóch podanych wartości i znaku działania.
/// </summary>
/// <param name="id">Łańcuch reprezentujący działanie.</param>
/// <param name="value1">Wartość pierwsza.</param>
/// <param name="value2">Wartość druga.</param>
/// <param name="result">Wynik operacji (zmieniany gdy błąd).</param>
/// <returns>Wyliczoną wartość.</returns>
public double Calculate(string id, double value1, double value2, ref EquResult result)
{
Dictionary<string, Function> dict = FindKey(id);
if (dict == null)
{
result = new EquResult(EquErrors.InvalidOperation);
return 0;
}
double calculated = 0;
try
{
calculated = dict[id](value1, value2);
if (double.IsInfinity(calculated)) result = new EquResult(EquErrors.ResultInfinity);
}
catch (System.Exception)
{
result = new EquResult(EquErrors.UserError);
}
return calculated;
}
/// <summary>
/// Szuka słownika posiadającego podane działanie.
/// </summary>
private Dictionary<string, Function> FindKey(string id)
{
foreach (Dictionary<string, Function> dict in symbols)
{
if (dict.ContainsKey(id)) return dict;
}
return null;
}
/// <summary>
/// Szuka następnego działania.
/// </summary>
/// <param name="equality">Równanie.</param>
/// <param name="start">Początek znalezionego działania</param>
/// <param name="lenght">Długość działania</param>
/// <param name="result">Wynik operacji (zmieniany gdy błąd)</param>
public void FindNext(string equality, out int start, out int lenght, ref EquResult result)
{
if ((start = equality.LastIndexOf(")")) != -1)
{
start += 1;
lenght = Regex.Match(equality.Substring(start), @"\D").Length;
return;
}
for (int i = symbols.Length - 1; i >= 0; i--)
{
start = FindNextByRank(equality, i, ref result);
if (start != -1)
{
Match r = Regex.Match(equality.Substring(start), @"\D+");
lenght = r.Length;
return;
}
}
result = new EquResult(EquErrors.InvalidOperation);
start = -1;
lenght = 0;
}
/// <summary>
/// Szuka kolejnego działania o podanej ważności
/// </summary>
/// <seealso cref="FindNext"/>
private int FindNextByRank(string equality, int rank, ref EquResult result)
{
int last = -1;
foreach (KeyValuePair<string, Function> pair in symbols[rank])
{
int found = equality.LastIndexOf(pair.Key);
if (found > last) last = found;
}
return last;
}
}
Jeśli ktoś przeczytał choć jeden listing (są tacy?) to pewnie zauważył, że używam jeszcze klasy EquResult. Postanowiłem nie wklejać jej i powiązanych kodu, ponieważ zajęłoby to tylko miejsce, a nic ciekawego w nich nie ma.
Przykłady użycia:
Używanie jest w miarę proste:
EQU_tree tree = new EQU_tree();
tree.CreateTree("2+2*2);
double d = tree.Calculate();
Obsługiwane jest również dodawanie własnych działań:
private double MOD(double value1, double value2)
{
return (int)value1 % (int)value2;
}
tree.AddFunction("%", MOD, 3);
dodaje funkcję wyliczającą modulo:
- '%' to identyfikator tej funkcji w równaniu (czyli informacja że zapis np 3%2 odnosi się do tej właśnie funkcji)
- MOD to funkcja pasująca do delegacji "Function"
- 3 to ranga ważności jeśli chodzi o kolejność wykonywania działań. Im niższa tym funkcja ważniejsza.

Też coś takiego napisałem
http://4programmers.net/C_sharp/Gotowce/Odwrotna_notacja_polska_-_gotowiec
:)