Obliczenie wyznacznika metodą LaPlacea

Rozwinięcie LaPlace'a jest jedną z najwygodniejszych i najszybszych metod obliczania wyznacznika macierzy kwadratowej wyższego stopnia. Wyznacznik tą metodą oblicza się zgodnie ze wzorem:

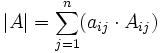
gdzie:
|A| - wyznacznik macierzy A
a_ij - element w i-tym wierszu i j-tej kolumnie
A_ij - dopełnienie algebraiczne elementu a_ij

Gotowy algorytm

Treść powyższego twierdzenia można zobrazować następującym pseudokodem:

wynik metodaLaplace (macierz, stopien)
{
    if ( stopien <= 2 ) { obliczenie wyznacznika z definicji }
    for ( kolumna = 0; kolumna < stopien; kolumna++ )
    {
        { przepisywanie nieskreślonych elementów macierzy do dopełnienia algebraicznego }
        wyznacznik += (-1)^(1+kolumna+1) * macierz[0][kolumna] * metodaLaplace (dopelnienie, stopien-1);
    }
    return wyznacznik;
}

<justify>Gotowy algorytm (podobnie zresztą, jak metoda) jest rekurencyjny, pamięć pod dopełnienia algebraiczne alokowana jest dynamicznie. Wyznacznik stopnia co najwyżej drugiego jest obliczany z definicji. Wykreślanie kolumny i przepisywanie nieskreślonych współczynników odbywa się w dwóch pętlach For. Całość prezentuje się następująco:</justify>

#include <stdio.h>
#include <stdlib.h>
#include <errno.h>
#include <math.h>

#define MAX_STOPIEN 100    /* Maksymalny stopień macierzy */

   long double** nowaMacierz (int stopien);
   void usunMacierz (long double** macierz);
   long double metodaLaplace (long double** macierz, int stopien);
   void anuluj (int nr_bledu);

int main (int argc, char* argv[])
{
   long double** macierz;
   int stopien;
   int nr_wiersza, nr_kolumny;

    printf("Proszę podać stopień macierzy n=");
    if ( !fscanf(stdin, "%d", &stopien) ) anuluj(EINVAL);
    macierz = nowaMacierz(stopien);
    for (nr_wiersza=0; nr_wiersza < stopien; nr_wiersza++)
        for (nr_kolumny=0; nr_kolumny < stopien; nr_kolumny++)
        {
            printf("A[%d,%d]=", nr_wiersza, nr_kolumny);
            if ( !fscanf(stdin, "%Lf", &macierz[nr_wiersza][nr_kolumny]) ) anuluj(EINVAL);
        }
    printf("det(A) = %Lf\n", metodaLaplace(macierz, stopien));
    usunMacierz(macierz);
    getchar();
    return 0;
}

 /* =====  Tworzy nową macierz kwadratową danego stopnia ===== */
long double** nowaMacierz (int stopien)
{
    long double** macierz;
    int nr_wiersza;

    if (stopien < 1 || stopien > MAX_STOPIEN) anuluj(EINVAL);
    if (!( macierz = (long double**) calloc(stopien, sizeof(long double*)))) anuluj(-1);
    if (!(*macierz = (long double* ) calloc(stopien*stopien, sizeof(long double)))) anuluj(-1);

    /* Przydzielone adresy komórek pamięci są segragowane, tak by utworzyły tablicę dwuwymiarową */
    for (nr_wiersza = 1; nr_wiersza < stopien; nr_wiersza++ )		
        *(macierz+nr_wiersza) = *(macierz+nr_wiersza-1) + stopien;
    return macierz;
}

/* ====== Zwalnia pamięć zajętą przez macierz ====== */
void usunMacierz (long double** macierz)
{
    free(*macierz), free(macierz);
    return;
}

/* ===== Oblicza wartość wyznacznika metodą rozwinięcia Laplace'a ===== */
long double metodaLaplace (long double** macierz, int stopien)
{
    long double** dopelnienie;    /* Dopełnienie algebraiczne danego elementu macierzy */
    int nr_wiersza, nr_kolumny;
    int nr_kolumny_dop, nr_kolumny_mac;
    long double det = 0.00;    /* Wartość wyznacznika macierzy */

    /* Wyznacznik stopnia co najwyżej 2. zostanie obliczony z definicji */
    if (stopien <= 2) return macierz[0][0] * (stopien>1 ? macierz[1][1] : 1) - (stopien>1 ? macierz[0][1] * macierz[1][0] : 0);
    dopelnienie = nowaMacierz(stopien-1);
    for (nr_kolumny = 0; nr_kolumny < stopien; nr_kolumny++)
    {
        for (nr_kolumny_dop = 0, nr_kolumny_mac = 0; nr_kolumny_dop < stopien-1; nr_kolumny_dop++, nr_kolumny_mac++)
        {
            nr_kolumny_mac += (nr_kolumny_mac == nr_kolumny ? 1 : 0);  /* Wykreślona kolumna macierzy jest pomijana... */
            for (nr_wiersza = 0; nr_wiersza < stopien-1; nr_wiersza++)
                dopelnienie[nr_wiersza][nr_kolumny_dop] = macierz[nr_wiersza+1][nr_kolumny_mac];
        }
        /* det = ?(aij * (-1)^i+j * Aij) */
        det += (macierz[0][nr_kolumny] * (long double) pow(-1.0, 1.0+nr_kolumny+1.0) * metodaLaplace(dopelnienie, stopien-1));
    }
    usunMacierz(dopelnienie);
    return det;
}

/* ===== Wyświetla treść błędu i wychodzi z aplikacji ===== */
void anuluj (const int nr_bledu)
{
    errno = nr_bledu != -1 ? nr_bledu : errno;
    perror("Nie udało się obliczyć wyznacznika");
    exit(errno);
    return;
}